El's Dimension

4-1) 전체 패턴 개수 유추

# Import libraries

import random as rd

import matplotlib.pyplot as plt

  필요한 라이브러리를 불러옵니다. 이 코드에는 무작위 값을 얻기 위한 Python 내장 라이브러리 random과 그래프를 통한 시각화를 위한 matplotlib 라이브러리를 사용했습니다.

# Case variety range

case_range=range(1,101)

# Each case's trial amount

case_trial=100

# Each case get 80 samples

samples=80

# List which will store results and draw it

result=[]

  이 프로그램은 패턴의 종류가 1개일 때부터 시작해서 100까지 올려보고 패턴의 개수 즉 패턴의 풀 별로 80번의 퍼즐을 무작위로 뽑는 것을 패턴 별로 100회 반복해서 평균을 내는 프로그램입니다. 따라서 이에 필요한 상수들을 먼저 정의했습니다.

# Case Variety given

for cases in (case_range):

    case=list(range(1,cases+1))

    partial_result=0

    # Each trial

    for trial in range (case_trial):

        observed=[]

        # Get 80 (samples) sample

        for sample in range (samples):

            observed.append(rd.choice(case))

        # Change list to set in order to get only first observed cases

        partial_result+=len(set(observed))

    # Get average

    result.append(partial_result/case_trial)

  앞에서 설명한 방식 그대로 구현을 했습니다. 첫 번째 for 문에서 패턴의 풀을 하나씩 늘려갑니다. 두 번째 for 문에서는 평균을 취하기 위해 한 패턴 풀을 100회 반복하기로 했습니다. 마지막 for 문은 rd.choice() 함수를 통해 첫 번째 for 문에서 제시된 숫자 풀에서 무작위로 숫자를 받아와 list에 채워 넣은 뒤 파일 유형을 중복을 허용하지 않는 set로 바꾼 뒤 원소의 개수를 최종 결과에 저장합니다. 이 최종 결과에는 패턴 풀이 1개~100개 일 때 80개의 값을 꺼낼 때 등장한 패턴의 개수들의 평균들이 저장되게 됩니다.

# Plot chart

plt.plot(case_range,result)

plt.plot(case_range,case_range)

plt.plot([0,case_range[-1]],[48,48],c="black")

plt.xlabel("Pattern variety [count]")

plt.ylabel("Patterns observed [count]")

plt.title("Average pattern observe ratio\n(when %s samples with each case %s trial)"%(samples,case_trial))

plt.legend(["Simulated result","Pattern all seen","48 observed pattern line"])

plt.grid(True)

plt.show()    

출력 결과

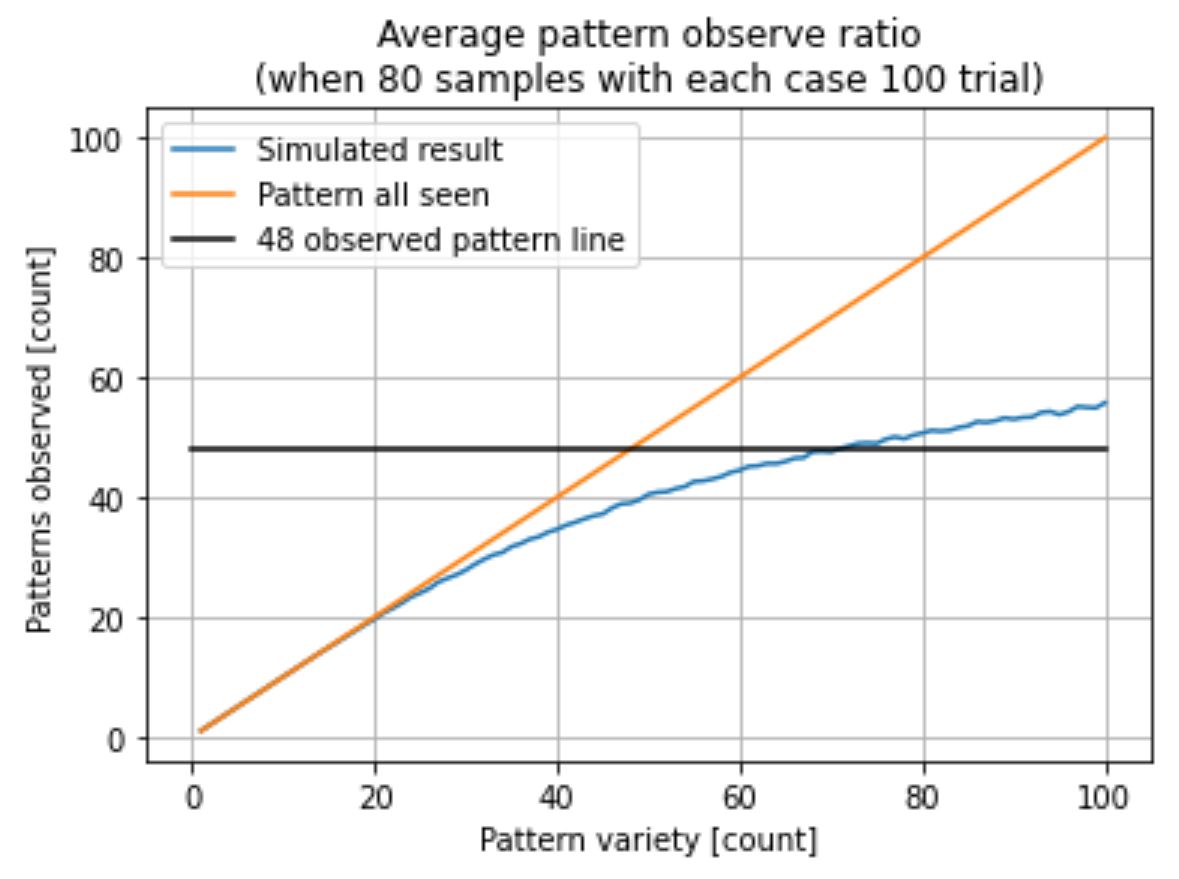
  파란색의 부들부들 떨리는 선이 시뮬레이션의 결과, 주황색 선은 모든 패턴을 발견했을 때와 대조를 위해 그은 보조선, 검은색 가로선은 이전의 프로그램에서 80개의 샘플에서 48 종류의 패턴을 봤던 분석 결과를 통해 전체 패턴의 개수를 유추하기 위해 그은 보조선입니다.

  검은색 선이 파란색 선과 교차하는 지점의 패턴 풀의 개수가 아마 미지의 전체 패턴 풀의 개수일 것입니다. 위의 프로그램의 결과상 약 70개의 패턴이 패턴 풀에 있을 때 80개의 샘플에서 48개의 패턴을 관측할 수 있다는 것을 알 수 있었습니다. 만약 이전 분석 결과가 모집단을 대표한다면 70 종류의 패턴이 있을 것이라고 생각하고 샘플을 수집해야 한다는 것을 알 수 있습니다.

4-2) 필요 샘플 개수 유추

  위의 프로그램을 통해 전체 패턴의 종류는 70개로 예상된다는 결론을 얻었습니다. 수학적으로 접근해 볼 때 만약 제가 예상치 못한 패턴이 있을 때 이 패턴을 빼고 예측 가능한 패턴을 뽑을 확률은 70/(70+1) 입니다. 이 연산을 반복한다면 2번 패턴을 뽑을 확률은 70/(70+1) * 70/(70+1) 일 것이고 n번 패턴을 뽑는다면 (70/(70+1))^n이 될 것입니다. 즉 n번을 뽑더라도 예측 범위 밖의 있을지 없을지 모르는 단 한 가지 경우의 수가 이 악물고 나오지 않는다는 의미는 예상 밖의 패턴이 존재할 가능성이 그만큼 낮아진다는 것을 의미하기도 합니다. 따라서(70/(70+1))^n 의 수식에서 n이 점점 커질수록 결과값이 낮아지게 되고 이 결과값을 예측밖의 패턴이 존재할 확률이라고 해석할 것입니다. 이 프로그램은 n을 하나씩 높여가며 결과값이 특정 값 이하가 되는 지점을 찾아서 적절한 샘플 개수 n을 찾는 프로그램입니다.

import matplotlib.pyplot as plt

import numpy as np

  시각화를 위한 matplotlib, 나중에 퍼센트로 표현하기 위해서 numpp.array 데이터형을 쓰기 위한 numpy 라이브러리를 불러옵니다.

#Values

diversity=70

reliability=0.001

probability=1

# Probability about observed (known, expected) pattern show

old_chance=diversity/(diversity+1)

# Start with 1 sample

counter=1

# Starting point (counter 0's value)

unseen_prob=[1]

  변수들과 초기 지점을 설정합니다.

# (diversity/(diversity+1))^n until it becomes so small that '+1''s exist probability can be neglected

while probability>reliability:

    probability*=(old_chance)

    unseen_prob.append(probability)

    counter+=1

counter-=1

print("With",counter,"sample, 1 unseen pattern exist probability:",probability)

print("(Below %s percent)"%(reliability*100))

  while 문을 통해 결과값이 0.1% 미만이 될 때까지 반복합니다. 이 반복문이 종료되면 놓치고 지나가는 패턴이 존재할 확률이 0.1%가 됨을 의미합니다. 분모에 왜 굳이 +1로 설정을 했는지 궁금해하실 수 있겠지만 1 이상의 어떤 자연수를 사용하더라도 더욱 빠르게 수렴하게 될 뿐입니다. 따라서 1을 넣어서 가장 천천히 수렴한다는 결과를 살펴 n이 최대인 최악의 상황을 고려할 수 있습니다.

unseen_prob=np.array(unseen_prob)*100

plt.plot(unseen_prob)

plt.xlabel("Sample count [each]")

plt.ylabel("Unseen pattern probability [%]")

plt.grid(True)

plt.title("When %s types of pattern expected,\

\n1 Unseen pattern exist probability\

\n(Simulate until probability below %s percent)"%(diversity,reliability*100))

plt.plot([diversity,diversity],[0,100],c="orange")

plt.plot([80,80],[0,100],c="green")

plt.legend(["Probability","%s samples line"%diversity,"80 samples line"])

plt.show()

  그래프로 출력을 하되 출력 전에 결과들에 모두 100을 곱해서 사람에게 익숙한 백분율로 보이도록 합니다.

출력 결과

With 487 sample, 1 unseen pattern exist probability: 0.0009998380510145163

(Below 0.1 percent)

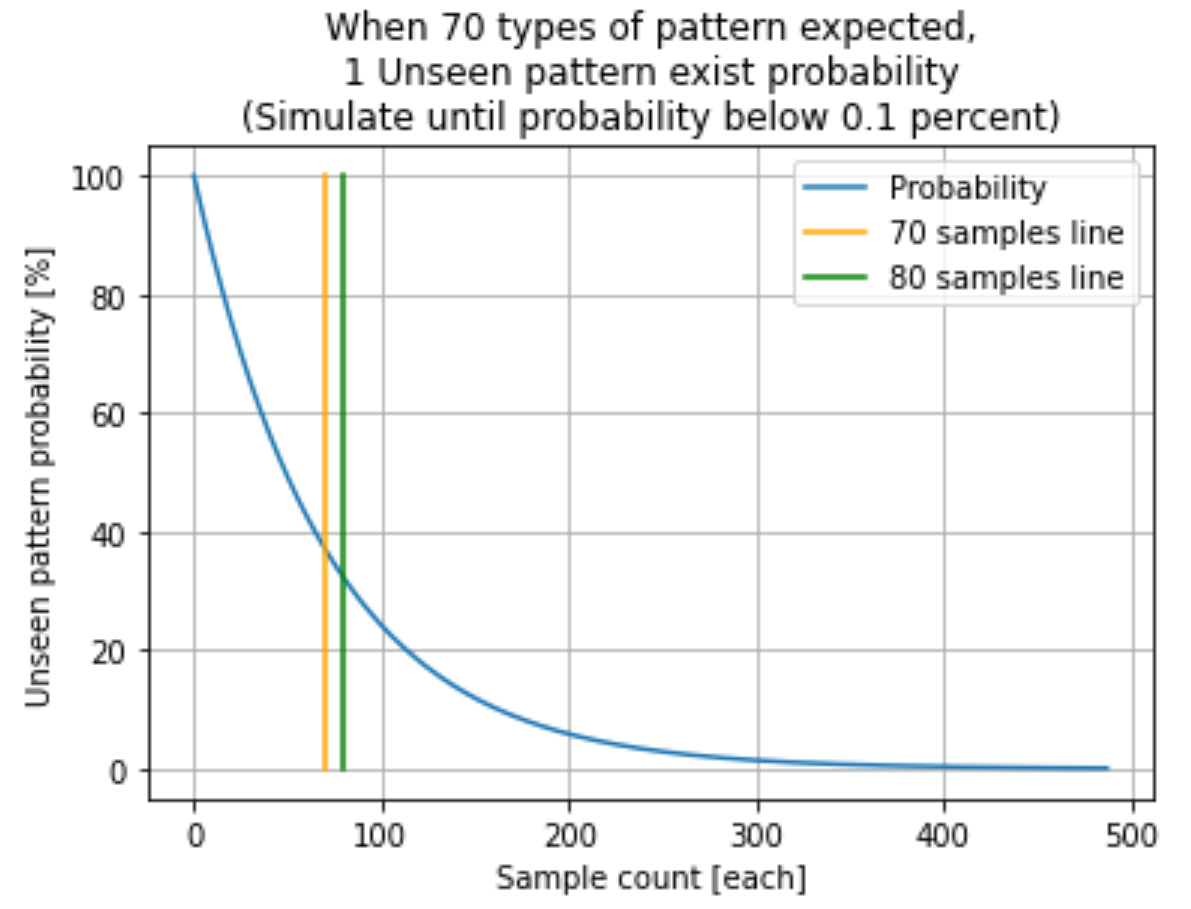
파란색 선이 계산 결과이며 주황색 선이 샘플 개수가 70개 일 때, 초록색 선이 이전 분석 때의 샘플 수인 80개를 나타내는 선입니다. 사실 주황색 선 왼쪽의 값들은 의미가 없는 값입니다. 애당초 패턴 풀이 70개인데 샘플이 70개도 되지 않는 것은 어불성설이기 때문입니다. 다만 계산 결과를 나타내는 그래프가 어떤 개형을 보이는지 알 수 있도록 처리를 하지 않고 내버려 두었습니다. 녹색 선과 파란색 선이 교차하는 지점의 확률을 확인한다면 샘플이 80개라면 35% 정도 확률로 미지의 패턴이 존재할 것이라는 것을 알 수 있습니다. 신뢰도가 100-35=65% 라면 그다지 좋은 결과라고 할 수 없다는 것을 알 수 있습니다. 이제 파란 선을 따라서 프로그램이 종료된 시점의 n을 확인해 봅시다. 이를 확인하기 위해 마지막 값은 특별히 print() 함수를 통해 출력을 하도록 했습니다. 샘플의 개수가 487개 정도일 때면 다른 값이 존재할 확률이 0.1% 미만이 된다는 것을 알 수 있었습니다. 따라서 저는 이번 분석에는 여유를 조금 줘서 약 500개의 샘플을 확보하기로 했습니다.

4-3) 영상 샘플 추출 프로그램

  대망의 주인공입니다. 이번 프로그램은 저도 처음 시도해보는 분석이기 때문에 결과에는 문제가 없었지만 여러 가지 부차적인 문제들이 있을 수 있습니다. 이를 감안하고 읽어주십시오.

# Driver Mount

# Only necessary on goole colab

from google.colab import drive

drive.mount('/content/gdrive')

  이제부터는 영상 파일을 올리고 프레임 이미지를 시험 삼아 저장하고 결과를 csv 파일로 저장해야 하기 때문에 Colab 환경에서는 드라이브를 마운트 해서 구글 드라이브에 액세스 할 수 있도록 합니다.

# Import libraries

import numpy as np

import matplotlib.pyplot as plt

import cv2 as cv

import csv

  cv2를 제외하고는 위의 두 프로그램에서도 사용한 라이브러리입니다. cv2는 이미지 및 영상 처리를 위한 OpenCV2 라이브러리입니다. 이번 프로그램에서 가장 중요한 역할을 맡은 라이브러리입니다. 영상 처리에 이 라이브러리를 선택한 이유는 슈퍼마리오 게임의 영상에서 코인들을 강조하는 예제 코드가 이 OpenCV2를 이용하고 있었기 때문입니다. 제가 원하는 기능과 흡사한 예제 코드였기 때문에 굉장히 큰 도움이 되었습니다.

  여러가지 값들을 미리 입력했습니다. .

# Set flags

save_p_frame = True # Save frames containing puzzle as jpg

fbf_p_tracker_save = True # Save frames containing puzzle and it's tracking as jpg

  이 두 값은 퍼즐이 있는 프레임을 찾았을 때 프레임의 이미지를 저장할지, 퍼즐 조각들을 찾아낸 것을 시각화 해주는 이미지를 저장할 지 설정하는 값들입니다. 저는 결과가 제대로 나왔는지 확인하기 위해 둘 다 True로 놓고 프로그램을 돌렸습니다.

# Set base directory (directory of this file on colab enviornment)

# When setting base_dir directory should end with \

# For colab '/content/gdrive/My Drive/'

base_dir="/content/gdrive/My Drive/"

  개인 컴퓨터에서 설치해서 사용하는 idle 환경에서는 기본적으로 py 파일이 있는 그 자리에 파일이 있으면 해당 파일의 이름을 주소로 설정해도 이를 자신에 대한 상대 주소로 인식하여 원하는 파일을 불러올 수 있습니다. 하지만 구글에서는 마운트 된 드라이브를 시작 지점으로 하는 절대주소 형식으로 파일의 위치를 지정해야 합니다. base_dir는 마운트 된 드라이브에 대한 주소를 미리 지정한 변수로 파일명 앞에 이를 붙여서 원하는 파일을 불러올 수 있도록 했습니다.

# Name of video file to

sample_video="sample_vid.mp4"

  샘플을 얻을 동영상의 이름입니다.

# Frame by frame threshold

min_fbf_thres=0.5

max_fbf_thres=0.8

fbf_method=cv.TM_CCOEFF_NORMED

  프레임에서 프레임을 넘어갈 때의 시행하는 분석의 방법과 역치값의 구간을 지정하는 부분입니다. 이 부분은 뒤에서 다루도록 하겠습니다.

# Piece_threshold

piece_thres=0.95

piece_method=cv.TM_CCOEFF_NORMED

  퍼즐 조각을 찾을 때의 역치값과 방법을 정의했습니다. 이 부분 또한 뒤에서 설명하겠습니다.

# Puzzle status finder sensitivity

sensitivity=60

  퍼즐의 패턴을 읽을 때 사용한 민감도라는 값입니다. 이 값이 사용될 때 설명드리도록 하겠습니다.

# Load puzzle piece templates

puzzle_piece=[]

puzzle_diversity=6 # Last origin has 6 types of puzzles

for puzzle_num in range (puzzle_diversity):

    pieces=[]

    for piece_num in range (2,10): # 2,3,4,5,6,7,8,9 pieces (piece 1 is blank)

        pieces.append(cv.imread(base_dir+"sample_template/%d%d.jpg"%(puzzle_num+1,piece_num)))

    puzzle_piece.append(pieces)

  이제 퍼즐 조각들의 템플릿을 불러오도록 합시다. 템플릿 이미지는 대조할 이미지를 의미합니다. 즉 여기서 불러온 퍼즐 조각의 템플릿을 퍼즐이 있는 이미지와 비교하여 퍼즐이 있는지 없는지 판단할 것입니다. 현재 라스트 오리진에는 1번부터 6번 퍼즐까지 있으며 각 퍼즐은 2번부터 9번 조각까지 존재합니다. 퍼즐 조각의 번호는 완성되었을 때 키보드 오른쪽의 숫자패드 숫자들을 각자의 번호로 가집니다. 즉 퍼즐이 완성되면 맨 윗줄에 7,8,9 조각, 가운데에 4,5,6 조각, 맨 아래에 빈칸과 2,3 조각이 존재하게 됩니다. 2중 for문으로 2번 퍼즐의 2번 조각인 22, 2번 퍼즐의 3번 조각인 23 … 식의 형태로 저장된 템플릿 이미지를 불러옵니다. 참고로 이 템플릿 이미지는 퍼즐 조각의 가운데 부분의 일부만을 저장했습니다. 경계선이 모호한 경우를 피하고 나중에 패턴을 읽기 용이하게 하기 위함입니다.

# BGR in list to track pieces

color=[(0,0,255),(0,255,0),(255,0,0),

       (0,200,200),(200,0,200),(200,200,0),

       (200,200,200),(255,255,255)]

  별로 중요한 부분은 아니고 나중에 퍼즐조각들을 찾은 것을 확인할 때 템플릿 부분의 경계를 강조할 색상을 미리 지정해 놓은 것입니다. 참고로 OpenCV2 에서는 RGB 형식이 아니라 BGR 형식으로 색을 다룹니다. 따라서 첫 번째 색상은 파란색이 아니라 빨간색입니다.

# Program starts from here

# List which will store puzzle number and puzzle status

sample=[]

# Load video with puzzles

cap=cv.VideoCapture(base_dir+sample_video)

# Value used for labeling

capture_cursor=1

# read first frame

ret,frame=cap.read()

template_frame=frame # frame of one step before

# run program until last frame is given

while cap.isOpened():

    ret,frame=cap.read()

    # Stop stream when there's no frame

    if not ret:

        print("Can't recieve frame (or stream ended)")

        break

  본격적으로 프로그램이 시작되는 부분입니다. cv.VideoCapture() 함수를 통해 비디오 파일을 불러오고 이를 cap이라고 하여 하나의 객체로 이용합니다. 앞으로는 이를 비디오 객체라고 하겠습니다. 비디오 객체의 .read() 함수는 해당 프레임의 유무 여부와 프레임의 정보를 반환합니다. 따라서 프레임이 없어질 때 적절하게 반복문을 종료하도록 해야 합니다. 이 경우에는 비디오 객체의 .isOpened() 함수를 통해 비디오 파일이 열려 있다면 계속해서 명령을 반복 수행하도록 되어있습니다만 프레임이 없어진다면 .read()의 반환값 ret가 False가 되며 break 명령을 수행하여 반복문을 탈출하게 됩니다.

  윗부분에서 제일 중요한 점은 우선 파일을 열어 프레임 정보를 받아오면 첫 프레임을 이전 프레임으로 저장해 놓는다는 점입니다. 그 뒤에 while 문에 들어갔을 때는 그 다음 프레임을 받아오기 때문에 while 문에 들어온 시점에는 첫 프레임이 이전 프레임인 template_frame에 저장되어 있고 현재 프레임인 두 번째 프레임이 frame에 저장되어 있다는 점입니다.

    # Compare with frame right before

    res=cv.matchTemplate(frame,template_frame,fbf_method)

    # Frames are same on size so only 1 res value returned

    if min_fbf_thres<res[0][0]<max_fbf_thres:

        # Start Analysis if this frame is 'properly' changed

        '''

        High relativity: continuous frame (not needed)

        Proper relativity : puzzle appeared (right after answer pop up)

        Low relativity : answer appeared (only answer shows up first) , puzzle pop off

        '''

        # If flag is given, save this frame

        if save_p_frame == True:

            cv.imwrite(base_dir+"frame%d.jpg"%capture_cursor,frame)

  중요한 부분입니다. 이전 프레임과 현재 프레임을 cv.matchTemplate() 함수를 통해 둘의 유사성을 대조합니다. 인간의 두뇌는 컴퓨터가 하지 못 하는 일을 굉장히 손쉽게 해냅니다. 인간에게 두 프레임을 놓고 이 둘이 비슷하냐고 묻는다면 연속된 장면인지 여부에 따라서 대답을 해 줄 것입니다. 하지만 컴퓨터에게 이 애매한 개념을 이해시키는 것은 굉장히 난이도가 있는 문제입니다. 다행히도 대단한 실력을 가진 프로그래머들께서 이미 이런 문제를 해결해 줄 함수들을 미리 만들어 놓았습니다. matchTemplate()에 이미지와 이 이미지에서 찾을 이미지인 템플릿 이미지, 그리고 이미지를 분석할 방법을 입력하면 템플렛 이미지를 이미지의 우상단부터 차례차례 비교하고 이 비교를 통해 나온 일종의 유사도를 나타내는 하나의 값을 반환합니다.

  유사도를 반환한다는 것만 알면 되지만 구체적으로는 일종의 대푯값을 구하는 과정입니다. 프레임의 픽셀들과 템플릿 이미지 사이의 모종의 연산을 통해 값을 구하게 되는데 앞에서 저는 아래와 같이 방법을 사용하겠다고 했습니다.

fbf_method=cv.TM_CCOEFF_NORMED

  여기서 주목할 부분은 뒤의 ‘NORMED’ 입니다. NORMED는 Normalized, 즉 표준화를 의미합니다. 만약에 유사도를 계산했는데 유사도가 4000이라고 하면 해당 연산에 대하여 정확한 이해를 가진 사람이 아니라면 저것이 무엇을 의미하는지, 높은 것인지 낮은 것인지 직관적으로 알기 힘듭니다. 표준화는 최댓값를 1로, 최솟값를 0으로 고정하여 모든 값을 0~1로 표현하도록 값을 수정하는 작업입니다. 비록 절대적인 대푯값을 알기 어려워지지만 상한치와 하한치를 모르더라도 상한에 대한 비율로 표현되는 점은 유사도라는 개념의 이해에는 훨씬 유리합니다.

  위의 프로그램은 if 문을 통해 이전 프레임과 현재 프레임의 유사도가 앞서 정의한 최소 역치와 최대 역치 사이에 들어왔을 때만 모종의 연산을 수행하도록 하고 있습니다. 즉 앞의 유사도의 의미를 고려한다면 너무 닮지는 않았지만 그렇다고 전혀 닮지 않은 것은 또 아닌 프레임에 대해서 작업을 하겠다는 의미입니다. 구태여 상한과 하한을 정하며 프로그래밍을 한 것은 다음과 같은 이유가 있습니다.

  저도 프레임 단위로 분석을 하면서 깨달은 점이지만 라스트 오리진의 슬라이드 퍼즐을 켜면 정답만이 우선 나오고 그 다음 섞인 상태의 슬라이드 퍼즐이 등장합니다. 이를 유사도 순서대로 분류하면 아래와 같습니다.

유사도 낮음 < 정답 먼저 팝업 < 퍼즐 팝업 (필요한 부분) < 연속된 이미지  < 유사도 높음

  따라서 정답이 먼저 팝업 되는 낮은 유사도의 프레임도 거르고 이전 장면과 거의 동일한 연속된 이미지의 프레임도 걸러야 퍼즐이 나와있는 원하는 프레임을 얻을 수 있기 때문에 상한과 하한을 정한 것입니다.

  참고로 유사도가 높은 쪽과 철충이 있는 6번 퍼즐이 나올 때의 유사도가 굉장히 가깝게 나옵니다. 이 부분을 적절하게 조절해야 6번 퍼즐이 제외되지 않습니다. 여기서도 철충은 절 귀찮게 만듭니다. 철충을 싫어해야 할 이유가 하나 더 늘어났습니다.

  # If flag is given, save this frame

        if save_p_frame == True:

            cv.imwrite(base_dir+"frame%d.jpg"%capture_cursor,frame)

  이렇게 찾은 프레임을 저장해 줍니다. frame1, frame2, … 순으로 저장이 됩니다.

출력결과 (frame1.jpg)

 

  모두가 익히 아는 그 슬라이드 퍼즐이 켜진 모습입니다.

        # List which will save positions of template (puzzle piece)

        piece_pos=[]

        # Find puzzle number

        for puzzle_num in range (puzzle_diversity): # Last Origin slide puzzle has 6 type of puzzle

            res=cv.matchTemplate(frame,puzzle_piece[puzzle_num][0],piece_method) # Compare with every 2nd puzzle piece

            min_val, max_val, min_loc, max_loc = cv.minMaxLoc(res)

            # If puzzle piece has matching sector in frame

  이제 이 퍼즐의 퍼즐 번호가 몇 번인지를 확인할 차례입니다. for 문을 이용하여 이 퍼즐에 1번 퍼즐의 2번 조각의 템플릿, 2번 퍼즐의 2번 조각의 템플릿 … 순으로 템플릿을 앞에서 했던 것과 동일한 방법으로 대조를 합니다. 이번에는 이미지와 템플릿의 크기가 다르기 때문에 가능한 모든 지점을 대조해야 하기 때문에 여러가지 유사도 값이 나오게 됩니다. 이 유사도의 데이터는 좌측 상단에서 우측 상단까지의 데이터 한 행, 좌측 상단 한 픽셀 아래부터 우측 상단 한 픽셀 아래까지 한 행…이런 식으로 저장이 되기 때문에 2차원 numpy.array()로 구성되어 있습니다. 이제 여기서 최솟값과 최댓값을 찾아내야 하는데 다행히도 OpenCV2는 이런 2차원 numpy.array()의 최소값, 최댓값, 최솟값의 좌표, 최댓값의 좌표를 찾아주는 함수가 있습니다. cv.minMaxLoc()이 바로 그 함수입니다.

            if max_val>piece_thres:

                piece_pos.append(max_loc)

                # If flag is given draw rectangle at template's position

                if fbf_p_tracker_save==True:

                    BGR,width,height = puzzle_piece[puzzle_num][0].shape[::-1]

                    cv.rectangle(frame,max_loc,(max_loc[0]+width,max_loc[1]+height),color[0],3)

                    cv.putText(frame,"piece"+str(2),(max_loc[0],max_loc[1]-10),0,1,color[0],2)        

                break

  유사도가 최대인 값을 가져와서 유사도가 역치 이상이라면 그 좌표를 저장하고 break 문을 통해 for 루프를 탈출합니다. 유사도가 높은 2번 조각이 있는 그 퍼즐 번호가 바로 프레임에 있는 퍼즐 이미지의 퍼즐 번호이기 때문입니다. 그리고 만약 fvf_p_tracker_save 가 True로 되어 있다면 frame 이미지 위에 템플릿과 유사도가 높았던 그 지점에 사각형을 그리고 몇 번 조각인지 저장합니다. 이렇게 하면 지금 프레임 이미지에는 2번 퍼즐 조각의 위치가 강조된 이미지가 저장되어 있습니다.

  추가로 여기서 중요한 트릭 중 하나는 puzzle_piece[puzzle_num][0].shape[::-1 ] 이 부분입니다. 저렇게 하면 퍼즐의 차원에 관한 정보를 역순으로 반환하게 됩니다. 지금 puzzle_piece[puzzle_num][0] 에는 퍼즐의 높이 (픽셀 행의 개수) 퍼즐의 길이 (픽셀 열의 개수) 마다 BGR로 나타내는 색상정보 값 3개가 있습니다. 만약에 흑백 이미지라면 BGR로 나타내는 것이 아니라 밝기에 대한 값 하나로만 묘사되기 때문에 2차원의 값이 반환되어 두 개의 변수로 충분하지만 컬러 이미지를 사용하는 저는 BGR에 대한 세 번째 변수가 있어야 .shape() 연산의 결과값을 모두 받을 수 있습니다. OpenCV2에서 제공하는 튜토리얼은 흑백 이미지에서 하는 과정을 보여주었기 때문에 저도 저걸 따라서 값 두 개로 결과값을 받으려다 무수한 에러의 요청에 마주쳤습니다.

        # Track puzzle pieces

        for piece_num in range (1,8): # Last Origin slide puzzle is 3 by 3 puzzle with 8 pieces

            res=cv.matchTemplate(frame,puzzle_piece[puzzle_num][piece_num],piece_method)

            min_val, max_val, min_loc, max_loc = cv.minMaxLoc(res)

            piece_pos.append(max_loc)

            # If flag is given draw rectangle at template's position

            if fbf_p_tracker_save==True:

                BGR,width,height = puzzle_piece[puzzle_num][piece_num].shape[::-1]

                cv.rectangle(frame,max_loc,(max_loc[0]+width,max_loc[1]+height),color[piece_num],3)

                cv.putText(frame,"piece"+str(piece_num+2),(max_loc[0],max_loc[1]-10),0,1,color[piece_num],2)  

        # If flag is given, save frame with rectangles

        if fbf_p_tracker_save==True:

            cv.imwrite(base_dir+'frame%d track.jpg'%capture_cursor,frame)

        capture_cursor+=1

  이제는 퍼즐 번호를 알고 있으니 해당 퍼즐 번호의 3~9번 조각을 대조시켜서 같은 방법으로 처리를 해줍니다. 이렇게 해서 나온 frame1 track.jpg는 다음과 같습니다.

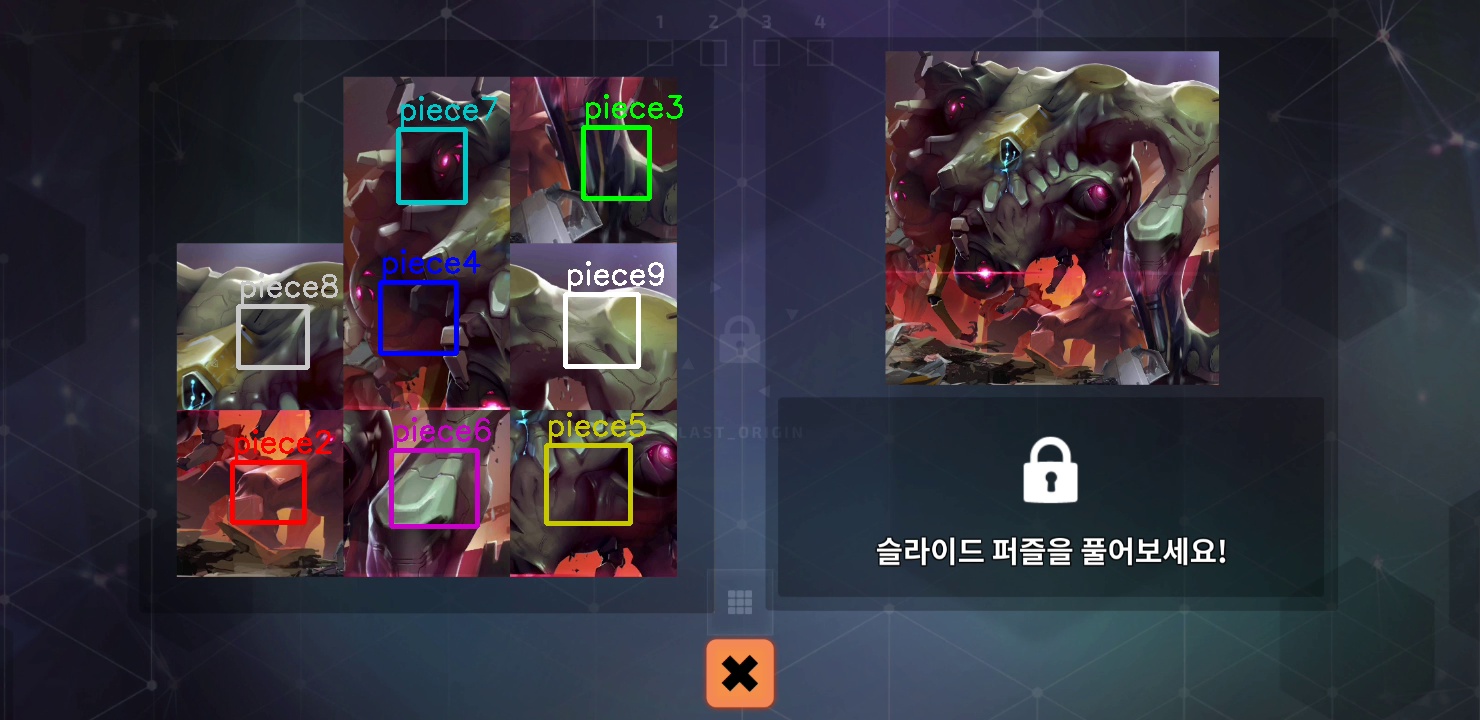
  앞에서도 언급했듯 템플릿 이미지는 퍼즐 조각의 가운데 쪽을 조금 잘라서 쓰고 있습니다. 그렇기 때문에 사각형도 퍼즐 조각의 한가운데 생긴 것을 볼 수 있습니다. 이제 퍼즐의 위치들을 원하는 형태의 데이터로 가공을 해보도록 하겠습니다.

 # Use pos to figure puzzle status

        XS=[]

        YS=[]

        for n in range (8):

            x,y=piece_pos[n][0],piece_pos[n][1]

            XS.append(x)

            YS.append(y)

        max_X, min_X = max(XS), min(XS)

        max_Y, min_Y = max(YS), min(YS)

        puzzle=np.zeros(9, dtype=int)

        for n in range(8):

            x=XS[n]

            y=YS[n]

            if min_Y<=y<=min_Y+sensitivity:

                pos=0

            elif max_Y-sensitivity<=y<=max_Y:

                pos=6

            else:

                pos=3

            if min_X<=x<=min_X+sensitivity:

                pos+=0

            elif max_X-sensitivity<=x<=max_X:

                pos+=2

            else:

                pos+=1

            puzzle[pos]+=(n+2)

        puzzle=list(puzzle)

        puzzle[puzzle.index(0)]='B'

        pattern=str(puzzle[0])

        for puzzle_cursor in range (1,9):

            pattern+=str(puzzle[puzzle_cursor])

        # save as puzzle number, puzzle pattern

        sample.append([puzzle_num+1,pattern])

    # Current frame will become past frame of future frame

    template_frame=frame

  이제 내용이 얼마 없어서 셀의 내용을 다 보여드렸습니다. 현재 퍼즐의 템플릿과 유사도가 가장 높은 지점들의 좌표들이 piece_pos 라는 list에 저장되어 있습니다. for문을 통해 빈칸을 제외한 8개의 값이 저장된 이 piece_pos의 X좌표와 Y좌표를 구분해서 XS, YS 두 개의 list에 각각 넣어줍니다. 그리고 XS와 YS의 최댓값과 최소값을 저장해 줍니다.

  이제 이 문제는 8개의 XS와 YS 값들을 낮은 집단, 중간 집단, 높은 집단으로 나누는 문제가 되었습니다. 지금 XS와 YS에는 퍼즐 조각의 순서대로 X 좌표, Y 좌표가 저장되어 있습니다. 이 즈음에서 제가 원하는 결과가 어떤 형태인지를 고려해야 합니다. 저는 퍼즐을 ‘789456B23’ 식으로 맨 위쪽 행부터 아래쪽 행으로, 좌측의 값부터 우측의 값 순으로 퍼즐 조각의 번호들을 저장하고 싶습니다. 그렇다면 각 퍼즐 번호가 위의 문자열인 str 형으로 저장될 때의 주소대로 퍼즐 번호를 할당하면 될 것입니다.

  XS YS에는 퍼즐 번호 순서대로 값들이 저장되어 있습니다. for 문을 통해서 하나씩 꺼냅니다. 일반적으로 원점의 위치는 좌하단이지만 OpenCV에서는 이미지의 좌상단이 원점입니다. 이미지의 우측에서 좌측으로 갈수록 X 좌표의 값이 커지고 이미지의 상단에서 하단으로 갈수록 Y 좌표의 값이 커집니다. 우선 Y좌표 값부터 확인합시다. If-elif-else 문을 통해 Y 값이 최소값과 최소값+sensitivity 사이라면, 즉 낮은 그룹에 속한다면 위치에 해당하는 pos 값에 우선 0을 줍니다. Y 좌표가 낮은 가장 위의 행은 str로 치환하면 0,1,2에 속하기 때문입니다. 마찬가지로 Y 좌표 값이 최대값과 최대값-sensitivity 사이라면 이번에는 pos를 6으로 정의합니다. Y가 가장 높은 최하단의 행은 6,7,8에 속하기 때문입니다. 이도저도 아닌 중간 그룹은 같은 원리로 pos 값을 3을 줍니다.

  같은 방식으로 X좌표에 대해서도 동일한 작업을 수행합니다. 다만 차이점은 이제는 pos= 형식으로 정의하는 것이 아니라 위에서 정해진 pos에 값을 더한다는 점입니다. 가장 낮은 그룹은 그대로, 가장 높은 그룹은 +2 중간 그룹은 +1을 주는 것입니다.

  이제 맨 위의 np.zeros()에 대해 설명할 시간입니다. np.zeros()는 0으로 채워진 numpy.array()를 반환하는 함수입니다. numpy.array()는 많은 것들이 일반적인 list와 유사합니다. 다만 list는 크기가 정해지지 않았지만 numpy.array()에서는 크기가 고정되어 있으며 한 종류의 데이터 타입을 넣을 수 있습니다. 사실 여기서 numpy.array()를 쓴 이유는 간편하게 제가 원하는 길이의 데이터 그룹을 만들 수 있기 때문입니다. 이제 pos를 좌표로 하는 pattern에 퍼즐 번호 순서대로 돌고 있는 n의 값에 2를 더해서 0에 더합니다. 이러면 n이 0인 첫 루프에서 2번 퍼즐 조각의 주소에 0 (원래 값) + 0 (n의 값) +2 (더해주는 값) = 2가 들어가게 됩니다. 이 과정을 반복하면 여기에 [7,8,9,4,5,6,0,2,3] 식으로 데이터가 저장이 됩니다. 이제 numpy.array()를 list로 바꿔주고 0을 “B”로 바꿔줍니다. 이제 [7,8,9,4,5,6,”B”,2,3] 식으로 데이터가 저장되어 있습니다. 첫 번째 값을 (컴퓨터 입장에서는 0번째) 꺼내서 문자형으로 바꿔주고 for 문을 돌려서 나머지 값들을 하나씩 꺼내서 첫 번째 값에 모두 더해줍니다. 문자열인 str 형에서 합연산을 수행하면 문자열을 그대로 뒤에 붙여주게 됩니다. 이제 퍼즐 번호와 문자열을 결과를 보여줄 list에 저장하고 다음 프레임에 대하여 동일한 작업을 수행합니다.

print("From video sample, %s sample puzzles were extracted"%(capture_cursor-1))

  출력 결과

From video sample, 500 sample puzzles were extracted

  마지막으로 몇 개의 샘플을 이 영상에서 얻었는지 확인해 줍니다.

# Save result as csv

with open (base_dir+"samples.csv",'w',newline='') as myfile:

    wr=csv.writer(myfile, quoting=csv.QUOTE_ALL)

    for cursor in range (len(sample)):

        wr.writerow(sample[cursor])

  그리고 이제 데이터를 csv로 저장해 줍니다.

  이제 나머지 분석은 지난번에 했던 분석코드에서 동일하게 수행했으니 그 부분은 생략하도록 하겠습니다.

  여기까지 읽어주셔서 정말로 감사합니다. 의견이나 다른 생각이 있으시다면 댓글을 달아주십시오. 다시 한 번 감사합니다.

# Driver Mount

# Only necessary on goole colab

 

from google.colab import drive

drive.mount('/content/gdrive')

 

  우선 Colab에서 구글 드라이브를 사용하기 위한 코드입니다. 이 코드를 실행하면 결과창에서 URL로 이동을 해서 승인 코드를 받아와서 입력하라고 합니다. 코드를 입력하면 Mounted at /content/gdrive 라는 메시지와 함께 Colab에서 구글 드라이브의 파일을 읽을 수 있게 됩니다.

 

# Size Factor and Flag check

row_size=3 #m

column_size=3 #n

 

plot_distribution_chart=True # Plot chart when enabled

save_csv=True # Save result_db and possible_case as csv type when enabled

load_csv=False # Load result_db and possible_case from existing csv files

 

  가로행과 세로열의 크기를 정의 해 줍니다. 라스트 오리진의 슬라이드 퍼즐은 3X3 사이즈이므로 3을 입력해 줍니다. 아래의 세 가지 변수는 참과 거짓만을 가지는 Boolean 타입의 변수입니다. 각각 그래프를 그릴지 여부, 데이터를 CSV 타입 파일로 저장할지, CSV 타입 파일로부터 데이터를 불러올지에 해당합니다. 저는 이 프로그램을 처음부터 돌릴 것을 상정하고 그래프를 그리고 결과 데이터를 CSV로 저장하되 외부로부터 결과 데이터를 불러오지는 않기로 했습니다.

# Import Libraries

import copy

import csv

import sys

import matplotlib.pyplot as plt

import numpy as np

  프로그래밍을 입문하는데 있어서 Python의 가장 큰 장점 중 하나로 꼽히는 외부 라이브러리들을 불러오도록 합시다. copy는 나중에 있을 Deepcopy를 위해서, csv는 CSV 타입 파일들의 처리를 위해, sys는 시스템 관련 값을 읽어오기 위해서 사용할 Python의 기본적으로 있는 함수입니다. matplotlib, numpy는 외부에서 설치하는 라이브러리로 각각 그래프를 그리는 연산, array라는 데이터 타입 및 수리연산을 위해 사용되는 라이브러리입니다. 상기할 점은 뒤의 두 라이브러리는 matplotlib.pyplot을 앞으로는 plt 라고 부르고 numpy를 np라고 줄여서 부르겠다는 점입니다.

  이제부터 보게 될 부분은 사용자가 만드는 사용자 지정 함수의 정의 과정입니다. 저는 우선 퍼즐을 만드는 함수 Puzzle_size 함수와 빈칸의 좌표를 입력하면 이 빈칸이 움직일 수 있는 자리들을 반환하는 Moveable 함수를 만들었습니다.

#Define Functions

def Puzzle_size(m=3, n=3):

    """Puzzle_size(m,n)

    Define size of puzzle

    m : size of single row (default 3)

    n : size of single column (default 3)

 

    3 by 3 for example, puzzle will follow order of

    right-side keyboard number pad

    """

    piece_num=1

    result=[]

    for cursor1 in range (n):

        row=[]

        for cursor2 in range (m):

            row.append(piece_num)

            piece_num+=1

        result.insert(0,row)

    result[n-1][0]="B" # B stands for blank piece that used for slide

    return result

  우선 가로행과 세로열의 크기를 입력 받고 각각 m과 n에 대응시킵니다. 퍼즐 조각의 번호는 1부터 시작하니 이를 piece_num 변수에 넣어주고 2중 for 문을 돌리며 퍼즐 조각 번호를 하나씩 넣어줍니다. 첫 번째 for 문은 결과에 들어갈 가로열을 하나씩 만들어 주고 두 번째 for 문에서 번호를 넣어주게 됩니다. 이 함수에 가로행과 세로열을 3,3을 입력한다면 [[7,8,9],[4,5,6],[B,2,3]] 식으로 퍼즐 1번이 들어가게 되는 좌하단이 빈칸을 의미하는 “B”라는 문자로 대체되는 list를 반환합니다. 이 퍼즐이 완성되었을 때의 상태로 키보드 우측의 숫자 패드나 라스트 오리진의 편성 창의 제대 위치 번호순으로 퍼즐 조각의 번호들을 지정한 것입니다.

def Moveable(pos_y, pos_x):

    """Moveable(pos_y, pos_x)

    Find moveable position of blank piece when position of blank piece is given

    Blank piece's position = puzzle[pos_y][pos_x]

    """

    global row_size

    global column_size

    result=[]

    # Up, Left, Right, Down 4 case

    if 0<=pos_y-1<column_size and 0<=pos_x<row_size: # Up

        result.append((pos_y-1,pos_x))

    if 0<=pos_y<column_size and 0<=pos_x+1<row_size: # Right

        result.append((pos_y,pos_x+1))

    if 0<=pos_y+1<column_size and 0<=pos_x<row_size: # Down

        result.append((pos_y+1,pos_x))

    if 0<=pos_y<column_size and 0<=pos_x-1<row_size: # Left

        result.append((pos_y,pos_x-1))

    return result

  Moveable 함수에서는 빈칸의 좌표를, 정확히는 인덱스를 입력하면 이동이 가능한 위치들의 인덱스들을 반환하는 함수입니다. global 키워드를 통해서 함수 외부에서 입력했던 가로행과 세로열의 값을 가져와서 B 좌표 주위 4칸의 좌표가 퍼즐의 범위를 초과하지 않는지 확인하여 퍼즐을 넘지 않는 값들만 반환하게 됩니다.

  외부의 라이브러리도 호출했고 사용자 정의 함수도 모두 정의했다면 본격적으로 돌아가는 부분을 짜봅시다. 우선 프로그램은 if – else 문으로 두 부분이 있습니다. 만약에 앞에서 load_csv를 True라고 정의하지 않았다면 처음부터 시뮬레이션을 돌리고 그렇지 않다면 외부의 데이터를 가져오도록 설정했지만 지금 코드는 외부의 CSV 데이터를 제대로 불러오지 못 합니다. 해결을 할 방법을 찾고 있습니다. 어쨌든 시뮬레이션 데이터를 처음부터 만들면 되는 문제이니 시뮬레이션 데이터를 만드는 코드를 보여드리겠습니다. 참고로 Colab 기준으로 이 부분을 실행하면 2시간이 살짝 안 되는 시간이 소요됩니다. 통발을 돌리듯이 코드를 돌리고 다른 일을 하면 되겠습니다.

# Program starts from here

# Start simulating every possible state using A-Star

if load_csv!=True:

    complete=Puzzle_size(row_size, column_size) # Compeleted puzzle (starting point)

    puzzle=[complete,column_size-1,0]

    # current puzzle state / position of Blank / position of Blank / Mother_puzzle

  우선 새로운 퍼즐을 만들고 퍼즐의 빈 칸의 위치를 list 안에 넣은 것을 puzzle 이라는 변수에 저장했습니다. 이제부터 시뮬레이션에서 가장 많이 움직인 단계의 퍼즐들은 모두 저런 형식으로 처리를 할 것입니다.

    possible_case=[] # Stock all of the possible cases

    result_db=[]

    # [ [ [puzzle_case/moter_puzzle],[...],[...]] with same # of blank move]

   A* 알고리즘은 경로와 비용을 모두 필요로 합니다. 사실 슬라이드 퍼즐을 클리어 하는 데 드는 이동 횟수가 비용의 역할을 수행할 것이고 0번 움직인 퍼즐로 1번 움직인 퍼즐들을 만들고 1번 움직인 퍼즐들로 2번 움직인 퍼즐들을 만드는 과정을 반복할 것이기 때문에 비용은 별도의 변수로 저장할 필요가 없습니다. 경로의 경우에는 단순히 최단 거리라는 비용만을 토대로 분석을 할 것이라면 따로 저장할 필요가 없겠지만 이 코드가 제대로 돌아간다는 것을 시연하기 위해서 n 번째 이동을 한 특정 퍼즐을 만드는데 쓰인 n-1 번째 퍼즐의 번호도 같이 기록을 하기로 했습니다.

    possible_case.append(puzzle[0])

    result_db.append([[puzzle[0],"M"]])

    most_moved_puzzles=[puzzle]

  possible_case 는 지금까지 만든 퍼즐들을 모두 담고 result_db에는 지금까지 만든 퍼즐과 그 퍼즐을 만드는데 쓰인 이전 단계의 퍼즐의 주소를 입력하도록 했습니다. 굳이 이 둘을 나눈 이유는 나중에 어떤 퍼즐이 다른 짧은 경로로 나온 적이 있는지 없는지 확인할 때 result_db 처럼 다중 리스트로 되어있으면 검색을 하기 불편하기 때문입니다. 매모리 관점으로는 손해지만 프로그램의 속도 측면에서는 이득이라고 생각을 하기 때문에 이런 식으로 코드를 짰습니다. 막상 글을 게시하려고 생각하니 result_db 에는 굳이 퍼즐의 정보를 저장할 필요가 없다는 것을 알게 되었습니다. 이래서 기획이 중요한 법입니다.

  또한 가장 많이 움직인 퍼즐은 지금으로는 당연히 초기상태 퍼즐 (0회 이동) 밖에 없습니다. 이를 most_moved_puzzle 이라는 list에 넣어줍니다.

    while len(most_moved_puzzles) !=0:

        partial_result=[] # Puzzles with same # of blank move

        next_most_moved_puzzles=[] # List which will be next most_moved_puzzles

        # Select each puzzle state

        for previous_state_cursor in range(len(most_moved_puzzles)):

            selected_puzzle=copy.deepcopy(most_moved_puzzles[previous_state_cursor])

            # Find puzzle's next possible states

            possible_case_by_move=[]

            future_blank_positions=Moveable(selected_puzzle[1],selected_puzzle[2])

            # Select each next possible state and move blank piece

            for next_blank in future_blank_positions:

                next_puzzle=copy.deepcopy(selected_puzzle)

                next_puzzle[0][next_puzzle[1]][next_puzzle[2]],next_puzzle[0][next_blank[0]][next_blank[1]]=next_puzzle[0][next_blank[0]][next_blank[1]],next_puzzle[0][next_puzzle[1]][next_puzzle[2]]

                next_puzzle[1],next_puzzle[2]=next_blank[0],next_blank[1]

                # Check whether its already found state or not

                if next_puzzle[0] not in possible_case:

                    possible_case.append(next_puzzle[0])

                    partial_result.append([next_puzzle[0],previous_state_cursor])

                    next_most_moved_puzzles.append(next_puzzle)

        # After finding next cases are done find future state from this case

        most_moved_puzzles=next_most_moved_puzzles

        result_db.append(partial_result) 

    # Final partial result is blank so delete that

    result_db.remove(result_db[-1])

  들여쓰기가 헛갈리지 않도록 하기 위해 while문이 모두 다 끝난 뒤에 설명을 달도록 하겠습니다. 프로그래밍에서 while 문은 무한루프를 만들 수 있어서 굉장히 위험하지만 지금처럼 얼마나 작업을 수행해야 하는지 모르는 경우에는 크게 도움이 됩니다.

  이 while문을 한 번 돌면 이전 상태에서 가장 많이 움직인 퍼즐들의 집합체인 list인 most_moved_puzzle 안의 퍼즐을 하나씩 꺼내서 moveable 함수에 넣어서 이동 가능한 빈칸의 위치들을 찾습니다. 이렇게 얻은 빈칸들의 위치를 토대로 원래 퍼즐로부터 Deepcopy를 수행해서 동일한 퍼즐을 복제하고 그 퍼즐에서 빈칸을 이동시키고 possible_case에 동일한 상태의 퍼즐이 있는지 확인하고 그렇지 않다면 possible_case에 이 퍼즐을 등록하고 결과에도 반영을 하고 이 퍼즐을 next_most_moved_puzzles 라는 다새로운 가장 많이 움직인 단계들을 담는 list에 넣어줍니다.

  most_moved_puzzle 안의 모든 퍼즐로 다음 단계의 퍼즐을 찾았다면, 즉 동일한 이동횟수의 퍼즐들로 한 번 더 움직인 퍼즐들인 next_most_moved_puzzles를 만들었다면 이 next_most_moved_puzzles를 새로운 most_moved_puzzle로 넣고 다시 while문의 앞으로 돌아가게 됩니다. 만약에 이 단계를 반복하다가 더 이상 새로운 퍼즐을 찾을 수 없다면 마지막에는 빈 list만이 most_moved_puzzle이 될 것이고 이 때가 되어야 while문을 종료합니다.

  정리하면 이 while문은 n번 이동한 퍼즐들로 n+1번 이동한 퍼즐들을 만들고 n+1번 이동한 퍼즐의 개수가 0이 될 때 (모든 경우를 확인했을 때) 까지 반복 수행하고 이동 횟수 별로 퍼즐들을 정리하는 것 입니다.

  시뮬레이션은 여기서 완료되고 이 아래가 저장된 외부의 CSV 데이터를 불러오는 부분입니다. 작동이 잘 되지 않는 부분이니 간단하게만 설명드리면 크기가 큰 CSV 데이터를 불러오기 위해서 크기 제한을 없애고 파일들을 불러오는 코드입니다. 현재 확인된 문제는 list 형식을 갖추지 못하고 str 형태의 문자열로 데이터가 불러와 지고 있습니다.

# When load_csv == True (when dataset exists)

else:

    csv.field_size_limit(sys.maxsize)

    result_db=[]

    with open('Result_DB.csv',newline='') as file:

        reader=csv.reader(file)

        for row1 in reader:

            for row2 in row1:

                result_db.append(row2)

    possible_case=[]

    with open('Possible_case.csv',newline='') as file:

        reader=csv.reader(file)

        for row1 in reader:

            for row2 in row1:

                possible_case.append(row2)

이렇게 만들어진 데이터를 확인해봅시다.

# This is total possible case of given condition slide puzzle

total_case=len(possible_case)

# Print the result

print(row_size,"by",column_size,"sized slide puzzle has",total_case,"possible cases")

print("Most complicated case requires at least",len(result_db)-1,"moves")

출력 결과

3 by 3 sized slide puzzle has 181440 possible cases

Most complicated case requires at least 31 moves

  3X3 슬라이드 퍼즐은 181,440 가지 경우의 수가 있고 가장 많은 이동 횟수를 가진 경우는 31번의 움직임을 가진 케이스입니다. 즉 3X3 슬라이드 퍼즐은 아무리 복잡해도 31번 움직이기만 하면 모두 풀 수 있다는 것입니다. 31이라는 숫자를 보니 저는 ‘슬라이드 퍼즐 알못’이었던 것 같습니다.

# Save datas as csv file

if save_csv==True:

    with open("Result_DB.csv",'w',newline='') as myfile:

        wr=csv.writer(myfile, quoting=csv.QUOTE_ALL)

        wr.writerow(result_db)

    with open("Possible_case.csv",'w',newline='') as myfile:

        wr=csv.writer(myfile, quoting=csv.QUOTE_ALL)

        wr.writerow(possible_case)

별로 중요한 코드는 아니고 대충 지금 만든 시뮬레이션 데이터를 CSV 타입 파일로 저장하겠다는 코드입니다.

# Plotting distribution bar chart

x=range (1,len(result_db))

y=[]

for moves in x:

    y.append(len(result_db[moves]))

if plot_distribution_chart==True:

    plt.bar(x,y)

    plt.xlabel("Required least movement")

    plt.ylabel("# of cases")

    plt.title("Least movement solution cases of "+str(row_size)+"x"+str(column_size)+" slide puzzle")

    plt.grid(True)

    plt.show()

  필요한 최소 이동 횟수들과 요구하는 이동 횟수가 동일한 퍼즐들의 개수를 바 그래프로 그리는 코드입니다.

출력 결과

# Average movement required

total_moves=0

for moves in x:

    total_moves+=len(result_db[moves])*moves

average_movement_required=total_moves/total_case

print("Average movement required is",average_movement_required)

출력 결과

Average movement required is 21.972398589065257

이를 토대로 평균을 계산해 보면 3X3 슬라이드 퍼즐은 평균 21.97 회의 움직임으로 풀 수 있다는 의미입니다.

이제 분석에 사용할 새로운 사용자 지정 함수를 만들어 봅시다. Counter 함수는 퍼즐의 상태에 대한 문자열 데이터를 “789456B23” 같은 형태로 넣어주면 해당 퍼즐을 푸는데 필요한 최소 이동 횟수를 반환해 주는 함수입니다.

  다만 이 함수를 보면 주석처리 되어버린 긴 코드가 있는데 처음에는 여기에 list를 넣더라도 이동 횟수들을 반환해 주는 부분을 같이 만들고자 했는데 막상 생각해보니 함수 외부에서 for 문으로 처리하면 되는 것이라서 기껏 코드를 짜 놓고 주석처리를 해서 사용하지 않기로 했습니다.

  Path_finder 함수는 Counter 함수와 앞 부분은 동일합니다. 정해진 형식의 문자열로 퍼즐에 대한 정보를 넣으면 우선 그 퍼즐의 possible_case의 인덱스를 호출합니다. 말하자면 좌표 혹은 (메모리 상의 주소가 아니라 일상 생활에서의) 주소를 불러오는 과정입니다. Possible_case와 result_db에 퍼즐의 정보가 쌓이는 순서는 같다는 점을 이용해서 이동한 횟수에 따라서 나누어서 저장된 redult_db에서의 위치를 찾은 뒤 result_db에 등록된 해당 퍼즐을 만든 퍼즐의 인덱스를 참조하여 최상위, 즉 퍼즐을 완성한 상태까지 역행하고 그 과정에서 지나가는 퍼즐들을 모두 저장해서 반환하는 함수입니다. 나무를 생각한다면 앞에서 시뮬레이션을 한 과정은 나무줄기부터 나뭇가지들을 뻗어 나가게 하는 과정이라면 이 과정은 나뭇가지 끝에서 다시 줄기로 역행하는 과정입니다.

# Functions defined under this comment can be used for further analysis

def Counter(puzzle):

    """Counter(puzzle)

    input puzzle like "789456B12" or multiple puzzles using list

    function will return least required movment

    """

    global row_size #m

    global column_size #n

    global possible_case

    global y

    # If single case is given

    if type(puzzle)==str:

        # make str as slide puzzle grid form

        target=[]

        letter_cursor=0

        for cursor1 in range (column_size):

            row=[]

            for cursor2 in range (row_size):

                try:

                    row.append(int(puzzle[letter_cursor]))

                except:

                    row.append(puzzle[letter_cursor])

                letter_cursor+=1

            target.append(row)

        # y has distribution information

        # Find target index and because possible_case has data ordered by minimum required movement

        # So with distribution data, target's minimum required movement can be calculated

        case_index=possible_case.index(target)

        cumulative_distribution=0

        distribution_cursor=0

        while case_index > cumulative_distribution:

            cumulative_distribution+=y[distribution_cursor]

            distribution_cursor+=1

        return distribution_cursor

    # If multiple cases are given

    # Same as single str type data are given but doing it repeatitive

    # This feature doesn't needed

    '''

    else:

        result=[]

        for single_puzzle in puzzle:

            # make str as slide puzzle grid form

            target=[]

            letter_cursor=0

            for cursor1 in range (column_size):

                row=[]

                for cursor2 in range (row_size):

                    try:

                        row.append(int(single_puzzle[letter_cursor]))

                    except:

                        row.append(single_puzzle[letter_cursor])

                    letter_cursor+=1

                target.append(row)

            # y has distribution information

            # Find target index and because possible_case has data ordered by minimum required movement

            # So with distribution data, target's minimum required movement can be calculated

            case_index=possible_case.index(target)

            cumulative_distribution=0

            distribution_cursor=0

            while case_index > cumulative_distribution:

                cumulative_distribution+=y[distribution_cursor]

                distribution_cursor+=1

            result.append(distribution_cursor)

        return result

    '''

def Path_finder(puzzle):

    """Path_finder(puzzle)

    input puzzle like "789456B12"

    will return cases that will lead to complete puzzle

    """

    # Get parameters and result from outside of function

    global row_size #m

    global column_size #n

    global possible_case

    global y

    global result_db

    # make str as slide puzzle grid form

    target=[]

    letter_cursor=0

    for cursor1 in range (column_size):

        row=[]

        for cursor2 in range (row_size):

            try:

                row.append(int(puzzle[letter_cursor]))

            except:

                row.append(puzzle[letter_cursor])

            letter_cursor+=1

        target.append(row)

    case_index=possible_case.index(target)

    cumulative_distribution=0

    distribution_cursor=0

    # If only it is not 0 which means if given puzzle is not completed puzzle

    if case_index!=0:

        # case_index = 1 (Solved puzzle) + y[0] + y[1] + ... + y[n] + coordinate

        # While state loops until y[n+1]

        while case_index > cumulative_distribution:

            cumulative_distribution+=y[distribution_cursor]

            distribution_cursor+=1

        # y[n+1] value should not be included

        cumulative_distribution-=y[distribution_cursor-1]

        # Completed (Solved puzzle) Case

        cumulative_distribution+=1

    # This is cooridnate of puzzle case in result_db

    # result_db[mother_state_dimension][mother_state_cursor]

    mother_state_dimension=distribution_cursor

    mother_state_cursor=case_index-cumulative_distribution # to get coordinate only

    # This list will stack solution of given puzzle case

    solution=[]

    # Append puzzle step by step

    # In result_db, each puzzle case has coordinate of their mother-case

    # So by rewinding steps, this function can show solution

    while mother_state_dimension>=0:

        solution.append(result_db[mother_state_dimension][mother_state_cursor][0])

        mother_state_cursor=result_db[mother_state_dimension][mother_state_cursor][1]

        mother_state_dimension-=1

    return solution

  이제 가장 중요한 부분입니다. 제가 궁금했던 것은 일반적인 3X3 슬라이드 퍼즐의 평균 최소 이동 횟수가 아니라 라스트 오리진에서 제공되는 슬라이드 퍼즐의 평균 최소 이동 횟수입니다. 일반적인 3X3은 라스트 오리진의 슬라이드 퍼즐을 포함하는 더 큰 집합이지 이 분석이 라스트 오리진의 슬라이드 퍼즐을 대변한다고 하기에는 어느 정도 차이가 있습니다. 그 정도가 어느 정도인지 파악하기 위해서 라스트 오리진 슬라이드 퍼즐의 샘플 데이터를 불러옵시다.

# Get samples data from in-game data

# Data has column of puzzle number and column of puzzle pattern

# Values have str type and utf-8-sig encoded

# Google colab enviornment requires mounted drive

# A Star generated puzzle and samples puzzle should have same size

with open ("/content/gdrive/My Drive/samples.csv",newline='',encoding='utf-8-sig') as file:

  reader=csv.reader(file)

  samples=list(reader)

print(samples)

출력 결과

[['1', '359B26478'], ['2', '8734B9265'], ['5', '4B5963728'], ['6', '83B975426'],…

  samples.csv 파일은 제가 직접 라스트 오리진의 슬라이드 퍼즐 80개를 캡쳐해서 MS 엑셀로 퍼즐 번호 한 열, 퍼즐의 상태를 “789456b23” 과 같은 문자열 형태로 한 열로 총 두 개 열로 입력한 파일입니다. 궁금하신 분들을 위해 첨부 파일로도 첨부를 했습니다.

  앞에서 본 CSV 파일을 읽어오는 것과 비슷합니다. 저 samples.csv 파일의 주소는 구글 드라이브에 바로 업로드 했을 때의 주소입니다.

# Check samples length (80)

len(samples)

출력 결과

80

앞에서 샘플 데이터가 80개가 있다고 했으니 제대로 불러와 진 것을 확인했습니다.

# Distribute puzzle number column and puzzle type column

samples_num=[]

samples_type=[]

for n in range (len(samples)):

  samples_num.append(samples[n][0])

  samples_type.append(samples[n][1])

이제 퍼즐 번호만 모은 list와 퍼즐의 상태의 정보를 모은 list로 파일을 나누어 주었습니다.

puzzle_num_count=len(set(samples_num)) # Last Origin's case = 6

  사실 이 변수는 중요한 변수는 아닙니다. 다만 라스트 오리진에는 1부터 6까지 퍼즐 번호가 있지만 차후에 확장될 수도 있기 때문에 이런 점을 고려하면 데이터 상에서 퍼즐 번호의 개수가 몇 개인지 파악하는 것이 중요하다고 생각해서 넣은 부분입니다. Python에서 set는 집합 연산을 지원하는 형식입니다. list 변수를 set 변수로 변환하면 list 내의 중복된 값들은 모두 하나로 통일이 됩니다. Samples_num은 앞에서 퍼즐 번호를 저장하는 list니 1~6 까지의 6 종류의 정수들만 있을 것입니다. 따라서 이 경우 해당 puzzle_num_count 변수의 값은 6이 될 것입니다.

# Puzzle appearance freequency (ratio) by puzzle number

puzzle_frequency_x=range(1,puzzle_num_count+1) # Last origin has 6 type of puzzle

puzzle_frequency_y=[]

for puzzle_num in (puzzle_frequency_x):

  puzzle_frequency_y.append(samples_num.count(str(puzzle_num)))

plt.bar(puzzle_frequency_x,puzzle_frequency_y)

plt.xlabel("Puzzle number")

plt.ylabel("Appearance")

plt.title("Puzzle appearance frequency by puzzle number\n(80 samples, 6 type of puzzle)")

plt.show()

출력 결과

  퍼즐 번호에 따른 등장 분포를 먼저 살펴보았습니다. 사실 저는 언제나 특정 퍼즐이 잘 나오지 않는 것 같다고 생각을 했습니다. 등장 확률이 동일하다면 각각 80/6 개 정도씩 나오야 하니 퍼즐 번호마다 13.33 개 정도의 값을 가져야 합니다. 지금 표를 봤을 때는 4번 퍼즐이 좀 많이 덜 나온 것 같기는 하지만 사실 이것만 가지고 4번이 덜 나온다고 주장하기에는 샘플이 많이 부족합니다. 기댓값을 기반으로 한 기대는 시행 횟수가 적을 때는 그다지 좋지 않은 결과를 불러올 때가 많습니다.

# Checking all puzzles are classified

sum(puzzle_frequency_y)

출력 결과

80

  위의 바들의 수치를 모두 합하면 80이 나오는 것을 확인했습니다. 굳이 확인을 해보지 않아도 당연한 것이지만 인코딩 형식 문제로 처음에는 csv 파일의 첫 번째 값을 이상하게 불러오는 문제를 겪었기 때문에 확인을 겸해서 수행한 연산이었습니다.

# Puzzle appearance frequency (ratio) by puzzle pattern (shuffled puzzle)

pattern_type_x=[]

pattern_type_y=[]

for puzzle_pattern in range(len(samples_type)):

  if samples_type[puzzle_pattern] not in pattern_type_x:

    pattern_type_x.append(samples_type[puzzle_pattern])

    pattern_type_y.append(samples_type.count(samples_type[puzzle_pattern]))

print("Observed pattern types are",len(pattern_type_x),"patterns")

plt.bar(pattern_type_x,pattern_type_y)

plt.gca().axes.get_xaxis().set_ticks([])

plt.xlabel("Puzzle pattern")

plt.ylabel("Appearance")

plt.title("Puzzle appearance frequency by puzzle pattern")

plt.show()

출력 결과

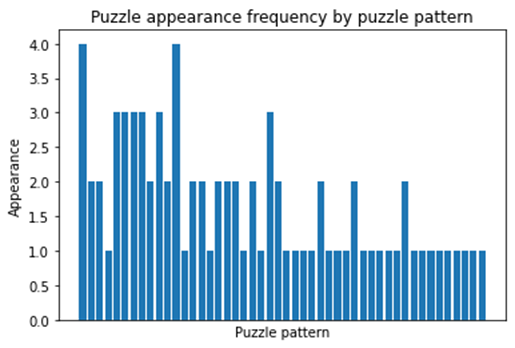
Observed pattern types are 48 patterns

다음은 패턴의 종류 별로 등장 빈도를 확인하는 막대 그래프입니다. 우선 패턴의 종류는 48가지 종류가 나왔으며 분포가 편향적이게 보일 수도 있지만 이 경우에도 샘플의 개수가 겨우 80개인 것이 문제가 됩니다. 제가 실력이 된다면 30분 정도 동안 슬라이드 퍼즐을 껐다 켰다 해서 영상을 만든 뒤 해당 영상에서 순간적으로 나오는 퍼즐들의 데이터를 읽어오게 하면 되겠지만 저는 아직 Python에서 영상을 다뤄본 적이 없습니다.

# Show each patterns required minimum movement to clear puzzle

pattern_clear_y=[]

for pattern in pattern_type_x:

  pattern_clear_y.append(Counter(pattern))

plt.bar(pattern_type_x,pattern_clear_y)

plt.gca().axes.get_xaxis().set_ticks([])

plt.xlabel("Puzzle pattern")

plt.ylabel("Required minimum movement")

plt.title("Required movement by puzzle pattern")

plt.show()

print("Average minimum required movement is",np.average(pattern_clear_y))

출력 결과

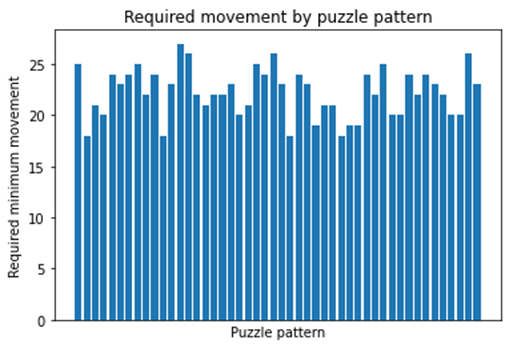
Average minimum required movement is 22.208333333333332

  각 패턴별로 클리어에 필요한 최소한의 이동 횟수는 다음과 같습니다. 이들의 값을 모두 더한 뒤 평균을 내면 22.20이라는 값이 나옵니다. 이 값은 라스트 오리진 슬라이드 퍼즐의 난이도를 이해하는 것에는 약간의 도움이 되기는 하지만 궁극적인 기대값은 개별 패턴의 난이도와 해당 패턴의 등장확률을 같이 고려한 것이 되어야 합니다.

# Show pattern ratio by required minimum movement

pattern_clear_frequency_y=[]

pattern_clear_frequency_x=range(min(pattern_clear_y),max(pattern_clear_y)+1)

for minimum_movement in pattern_clear_frequency_x:

  pattern_clear_frequency_y.append(pattern_clear_y.count(minimum_movement))

plt.bar(pattern_clear_frequency_x,pattern_clear_frequency_y)

plt.xlabel("Minimum clear movement")

plt.ylabel("Amount of Pattern")

plt.title("Each minimum clear movement's pattern types")

plt.show()

출력 결과

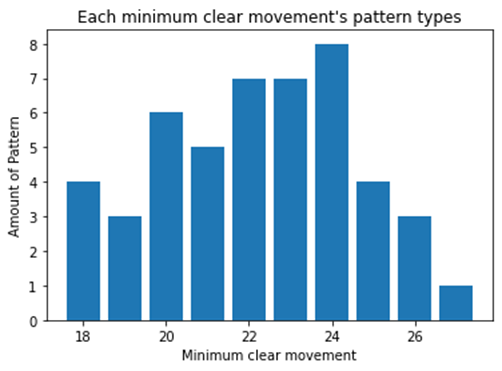
  결론을 내기에 앞서서 위의 막대 그래프에서 같은 클리어에 필요한 최소 이동 횟수를 가진 패턴들을 모아서 개수를 세어 보면 위와 같은 막대 그래프로 정리가 됩니다. 평균은 22 정도였지만 가장 빈도가 많이 나오는 최빈값은 24 였으며 중앙값은 22.5 정도입니다.

# Sample distribution by minimum clear movement

sample_distribution=np.zeros(len(pattern_clear_frequency_x),dtype="int")

base=min(pattern_clear_frequency_x)

for sample in samples_type:

  sample_distribution[Counter(sample)-base]+=1

print(sum(sample_distribution))

plt.bar(pattern_clear_frequency_x,sample_distribution)

plt.xlabel("Minimum clear movement")

plt.ylabel("Amount of sample")

plt.title("Last Origin slide puzzle's \n minimum clear movement distribution")

plt.show()

출력 결과

80

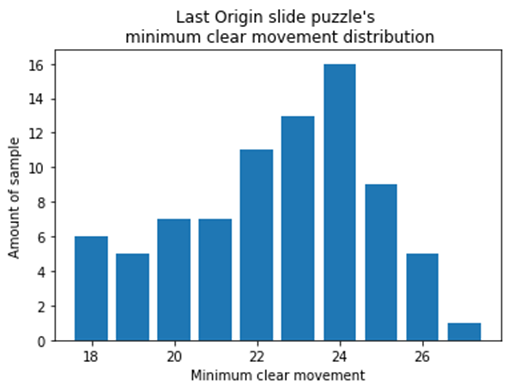
  맨 처음에 시뮬레이션을 마치고 나서 분포를 보여준 것처럼 패턴별이 아닌 샘플별로 필요한 최소 이동 횟수의 분포를 나타낸 막대 그래프입니다.

# With each patterns appearance probability, calculate average required minimum movement in last origin slide puzzle

total_required_minimum_movement=0

for cursor in range (len(pattern_type_y)):

  total_required_minimum_movement+=(pattern_type_y[cursor]*pattern_clear_y[cursor])

last_origin_average_required_minimum_movement=total_required_minimum_movement/len(samples)

print("Last Origin slide puzzle's average required minimum movement is",last_origin_average_required_minimum_movement)

출력 결과

Last Origin slide puzzle's average required minimum movement is 22.4625

  이제 결론을 내봅시다. 패턴의 등장 빈도와 패턴을 클리어 하는데 필요한 최소 이동 횟수를 고려했을 때 80개의 샘플을 클리어 하는데에는 평균적으로 22.46 회의 움직임이 필요하다는 것을 알 수 있습니다. 만약 80개의 샘플이 모집단을 잘 대변한다면 22~23번 정도로 퍼즐을 클리어 할 수 있는 분들은 가장 효율적인 클리어 방법으로 퍼즐을 풀고 계신 분들입니다. 오늘 패치 때 나온 퍼즐을 클리어 할 때 30번 넘게 움직인 저는 상상도 하지 못 할 일입니다.

  사실 여기까지가 궁금했던 내용이지만 혹시 특정 퍼즐 번호 별로 패턴이 할당되어 있는 것은 아닌가 하는 의문이 생겼습니다.

# Classifiy puzzles by puzzle number

pattern_classified=[[],[],[],[],[],[]]

for cursor in range (len(samples)):

    pattern_classified[int(samples[cursor][0])-1].append(samples[cursor][1])

  그것을 알아보기 위해서 이번에는 각 퍼즐 번호별로 보유한 패턴들의 list를 추려보았습니다.

# Print each puzzle numbers variety of pattern types

pattern_count=[]

for puzzle_number in range (0,puzzle_num_count):

    pattern_count.append(len(set(pattern_classified[puzzle_number])))

    print("Puzzle",puzzle_number+1,"has",pattern_count[puzzle_number],"patterns")

plt.bar(range(1,puzzle_num_count+1),pattern_count)

plt.xlabel("puzzle number")

plt.ylabel("puzzle pattern variety")

plt.title("Puzzle pattern variety by puzzle number")

plt.show()

출력 결과

Puzzle 1 has 11 patterns

Puzzle 2 has 16 patterns

Puzzle 3 has 12 patterns

Puzzle 4 has 7 patterns

Puzzle 5 has 13 patterns

Puzzle 6 has 15 patterns

  4번 퍼즐이 조금 수상한 결과가 나오기는 했는데 샘플의 개수가 적어서 그런 것일수도 있다고 생각합니다. 중요한 것은 퍼즐 번호들이 가진 패턴들이 교집합 여부입니다.

# Similarity Matrix

similarity_matrix=[]

for cursor_select in range (puzzle_num_count):

    similarity_row=[]

    for cursor_compare in range (puzzle_num_count):

        similarity_row.append(len(set(pattern_classified[cursor_select])&set(pattern_classified[cursor_compare])))

    similarity_matrix.append(similarity_row)

print("Similarity Matrix \n")

print(np.array(similarity_matrix))

출력 결과

Similarity Matrix

[[11  4  0  2  2  2]

 [ 4 16  2  2  5  3]

 [ 0  2 12  1  2  2]

 [ 2  2  1  7  2  0]

 [ 2  5  2  2 13  4]

[ 2  3  2  0  4 15]]

  위의 출력 력과는 읽는 법은 다음과 같습니다. 첫 번째 행의 숫자들은 1번 퍼즐과 1번퍼즐의 패턴의 교집합의 개수, 1번과 2번의 교집합의 개수, 1번과 3번의 교집합의 개수… 순으로 나아갑니다. 동일하게 두 번째 행은 2번과 1번, 2번과 2번, 2번과 3번… 순으로 나아가게 됩니다. 즉 좌상단에서 우하단으로 가로지르는 대각선은 자기자신과 자기자신에 대한 교집합이기 때문에 가장 수가 크고 그 주위의 값들은 자기와 다른 집합 사이의 교집합의 개수를 표현하는 숫자입니다. 만약에 여기서 자기 자신에 대한 값을 제외한 다른 모든 값이 0이 나왔다면 퍼즐 번호별로 보유한 패턴이 다르다고 해석할 수 있겠지만 그렇지 않은 것을 보아 퍼즐 번호와 패턴 사이에 반드시 상관관계가 있을 것이라고 판단할 수는 없음을 확인할 수 있습니다.

  그래서 저에게 슬라이드 퍼즐을 어떻게 해야 잘 풀 수 있냐고 물어볼 수도 있을 것입니다. 그런 분들을 위해서 보너스로 위에서 사용하지는 않았던 Path_finder 함수를 시연해 보고자 합니다.

# Check most complicated puzzle clear

most_complicated=Path_finder(pattern_type_x[pattern_clear_y.index(max(pattern_clear_y))])

print(most_complicated)

  가장 복잡했던 패턴을 불러와서 Path_finder 함수에 넣고 출력했습니다.

출력 결과

[[[9, 'B', 6], [3, 5, 8], [2, 4, 7]], [[9, 5, 6], [3, 'B', 8], [2, 4, 7]], [[9, 5, 6], ['B', 3, 8], [2, 4, 7]], [[9, 5, 6], [2, 3, 8], ['B', 4, 7]], [[9, 5, 6], [2, 3, 8], [4, 'B', 7]], [[9, 5, 6], [2, 'B', 8], [4, 3, 7]], [[9, 5, 6], ['B', 2, 8], [4, 3, 7]], [['B', 5, 6], [9, 2, 8], [4, 3, 7]], [[5, 'B', 6], [9, 2, 8], [4, 3, 7]], [[5, 6, 'B'], [9, 2, 8], [4, 3, 7]], [[5, 6, 8], [9, 2, 'B'], [4, 3, 7]], [[5, 6, 8], [9, 2, 7], [4, 3, 'B']], [[5, 6, 8], [9, 2, 7], [4, 'B', 3]], [[5, 6, 8], [9, 'B', 7], [4, 2, 3]], [[5, 6, 8], [9, 7, 'B'], [4, 2, 3]], [[5, 6, 'B'], [9, 7, 8], [4, 2, 3]], [[5, 'B', 6], [9, 7, 8], [4, 2, 3]], [[5, 7, 6], [9, 'B', 8], [4, 2, 3]], [[5, 7, 6], ['B', 9, 8], [4, 2, 3]], [['B', 7, 6], [5, 9, 8], [4, 2, 3]], [[7, 'B', 6], [5, 9, 8], [4, 2, 3]], [[7, 9, 6], [5, 'B', 8], [4, 2, 3]], [[7, 9, 6], [5, 8, 'B'], [4, 2, 3]], [[7, 9, 'B'], [5, 8, 6], [4, 2, 3]], [[7, 'B', 9], [5, 8, 6], [4, 2, 3]], [[7, 8, 9], [5, 'B', 6], [4, 2, 3]], [[7, 8, 9], ['B', 5, 6], [4, 2, 3]], [[7, 8, 9], [4, 5, 6], ['B', 2, 3]]]

  list 형의 문제점 중 하나는 이렇게 다중 list 에서는 가독성이 그다지 좋지 못 하다는 점입니다. 맨 앞에서 불러온 numpy의 array형으로 출력해서 가독성을 좋게 다시 보여드리겠습니다.

# Print as np.array for visability

for puzzle in range(len(most_complicated)):

  print("Step",puzzle)

  print(np.array(most_complicated[puzzle]),"\n")

출력 결과

Step 0

[['9' 'B' '6']

 ['3' '5' '8']

 ['2' '4' '7']]

Step 1

[['9' '5' '6']

 ['3' 'B' '8']

 ['2' '4' '7']]

Step 2

[['9' '5' '6']

 ['B' '3' '8']

 ['2' '4' '7']]

Step 3

[['9' '5' '6']

 ['2' '3' '8']

 ['B' '4' '7']]

Step 4

[['9' '5' '6']

 ['2' '3' '8']

 ['4' 'B' '7']]

Step 5

[['9' '5' '6']

 ['2' 'B' '8']

 ['4' '3' '7']]

Step 6

[['9' '5' '6']

 ['B' '2' '8']

 ['4' '3' '7']]

Step 7

[['B' '5' '6']

 ['9' '2' '8']

 ['4' '3' '7']]

Step 8

[['5' 'B' '6']

 ['9' '2' '8']

 ['4' '3' '7']]

Step 9

[['5' '6' 'B']

 ['9' '2' '8']

 ['4' '3' '7']]

Step 10

[['5' '6' '8']

 ['9' '2' 'B']

 ['4' '3' '7']]

Step 11

[['5' '6' '8']

 ['9' '2' '7']

 ['4' '3' 'B']]

Step 12

[['5' '6' '8']

 ['9' '2' '7']

 ['4' 'B' '3']]

Step 13

[['5' '6' '8']

 ['9' 'B' '7']

 ['4' '2' '3']]

Step 14

[['5' '6' '8']

 ['9' '7' 'B']

 ['4' '2' '3']]

Step 15

[['5' '6' 'B']

 ['9' '7' '8']

 ['4' '2' '3']]

Step 16

[['5' 'B' '6']

 ['9' '7' '8']

 ['4' '2' '3']]

Step 17

[['5' '7' '6']

 ['9' 'B' '8']

 ['4' '2' '3']]

Step 18

[['5' '7' '6']

 ['B' '9' '8']

 ['4' '2' '3']]

Step 19

[['B' '7' '6']

 ['5' '9' '8']

 ['4' '2' '3']]

Step 20

[['7' 'B' '6']

 ['5' '9' '8']

 ['4' '2' '3']]

Step 21

[['7' '9' '6']

 ['5' 'B' '8']

 ['4' '2' '3']]

Step 22

[['7' '9' '6']

 ['5' '8' 'B']

 ['4' '2' '3']]

Step 23

[['7' '9' 'B']

 ['5' '8' '6']

 ['4' '2' '3']]

Step 24

[['7' 'B' '9']

 ['5' '8' '6']

 ['4' '2' '3']]

Step 25

[['7' '8' '9']

 ['5' 'B' '6']

 ['4' '2' '3']]

Step 26

[['7' '8' '9']

 ['B' '5' '6']

 ['4' '2' '3']]

Step 27

[['7' '8' '9']

 ['4' '5' '6']

 ['B' '2' '3']]

총 27번의 움직임이 필요하다고 합니다.

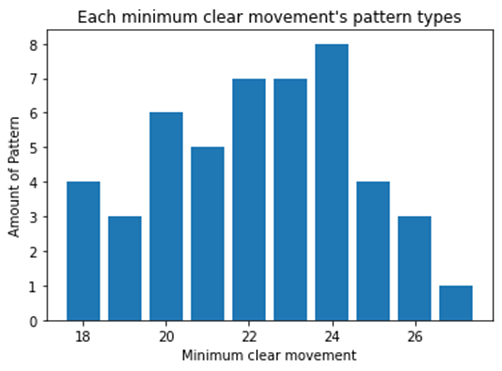
  위의 클리어에 필요한 최소 이동 횟수의 분포도 그래프를 다시 가져와 봤습니다. 가장 복잡한 사례의 경우에는 단 1번 등장한 27번의 이동이 필요한 퍼즐이었던 것을 확인했고 27번의 움직임만에 퍼즐을 풀 수 있는 것도 확인했습니다.

  여기까지 읽어주셔서 정말로 감사합니다. 초보적인 수준의 프로그래밍 실력이지만 궁금했던 것을 조금이나마 풀어서 재밌었고 의견이나 다른 생각이 있으시다면 댓글을 달아주십시오. 다시 한 번 감사합니다.